Tính Đường Cao Tam Giác Đều Kèm Công Thức
Đường cao là một trong những đặc trưng quan trọng của hình tam giác. Nó không chỉ giúp tính toán diện tích, chu vi mà còn liên quan đến nhiều bài toán khác. Trong bài viết này, chúng ta sẽ tìm hiểu cách tính đường cao của một tam giác đặc biệt – tam giác đều cũng như những thông tin hữu ích khác dành cho bạn.
Tam giác đều là gì?
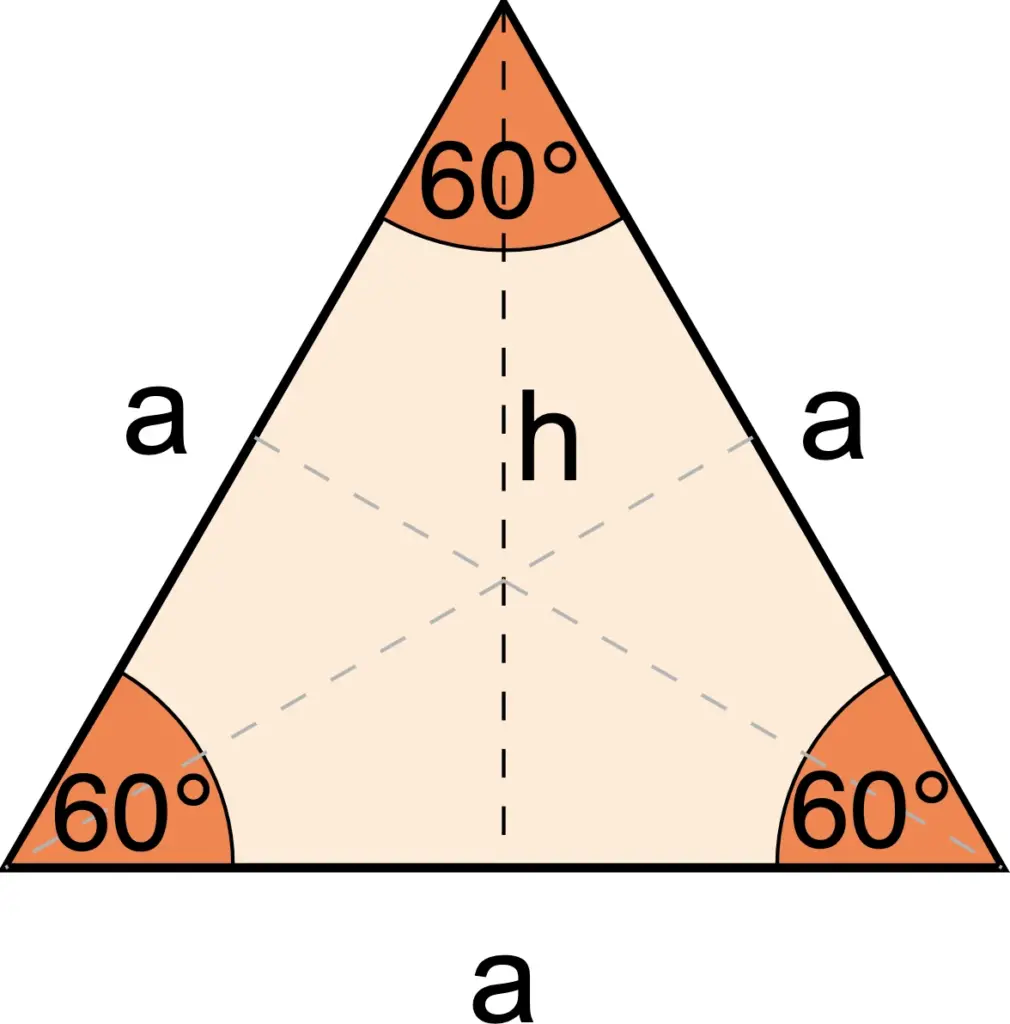
Tam giác đều là một loại tam giác đặc biệt, trong đó tất cả ba cạnh đều bằng nhau và ba góc của tam giác đều bằng 60 độ. Nhờ tính chất đối xứng, tam giác đều có nhiều ứng dụng trong thiết kế, kiến trúc và nghệ thuật.
Các đặc điểm của tam giác đều
Ngoài ba cạnh bằng nhau, tam giác đều còn có những đặc điểm sau:
- Có ba đường cao bằng nhau
- Có ba đường trung tâm bằng nhau
- Có tam giác gương (tam giác nhỏ trong tam giác lớn) cân đối hoàn hảo
Những tính chất này giúp việc tính toán trên tam giác đều trở nên đơn giản hơn so với các loại tam giác khác.
Công thức tính chiều cao tam giác
Công thức tính chiều cao tam giác thường
Chiều cao của một tam giác là đoạn thẳng kẻ vuông góc từ một đỉnh xuống đáy đối diện. Công thức tính chiều cao của một tam giác thường như sau:
h = (2 * S) / a
hoặc
$$h = \frac{2S}{a}.$$
Trong đó:
- h là chiều cao
- S là diện tích của tam giác
- a là cạnh đáy (cạnh đối diện với đỉnh mà chiều cao kẻ xuống)
Sử dụng định lý Pythagoras trong tam giác vuông
$$a^2 = b^2 + c^2$$
=> $$h = \sqrt{b^2 – \left(\frac{2}{a}\right)^2}.$$
Công thức tính chiều cao tam giác đều
Đối với tam giác đều, công thức tính chiều cao được đơn giản hóa nhờ tính chất đối xứng của nó. Chiều cao của tam giác đều được tính bằng cách:
h = (a * sqrt(3)) / 2
hoặc
$$h = a\frac{{\sqrt 3 }}{2}.$$
Trong đó:
- h là chiều cao
- a là cạnh của tam giác đều
Công thức này xuất phát từ việc tam giác đều có thể chia thành hai tam giác vuông cân bằng nhau, với chiều cao là một trong các cạnh vuông góc.
Chứng minh công thức trên
Xét một tam giác vuông bất kỳ trong tam giác đều, với cạnh huyền a (cũng là một cạnh của tam giác đều) và hai cạnh kia có độ dài a/2 (vì chúng là độ dài của đường chia tam giác đều thành hai tam giác vuông).
Theo định lý Pythagoras, ta có:
$$\left( \frac{a}{2} \right)^2 + h^2 = a^2$$
Giải phương trình trên, ta được:
$$ \frac{a^2}{4} + h^2 = a^2 $$
$$h^2 = a^2 – \frac{a^2}{4}$$
$$h^2 = \frac{3a^2}{4}$$
Để tìm h , chúng ta lấy căn bậc hai của cả hai bên của phương trình:
$$h = \sqrt{\frac{3a^2}{4}} => h = a\frac{{\sqrt 3 }}{2}.$$
Làm sao để tính chiều cao của một tam giác đều?
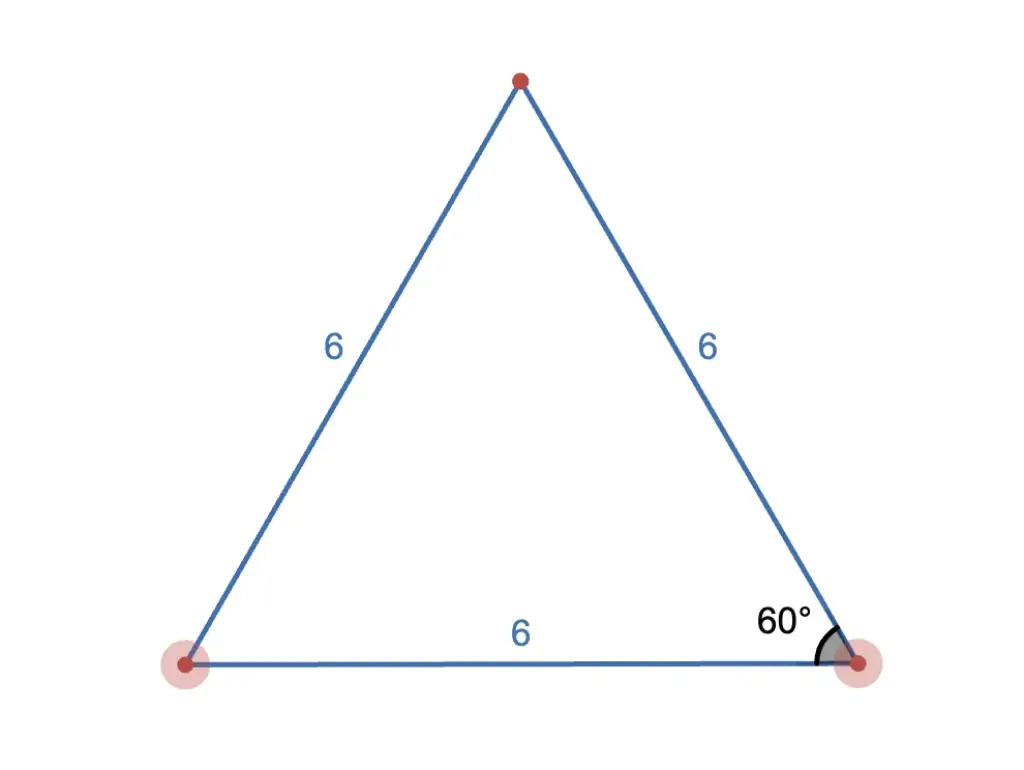
Bước 1: Xác định cạnh của tam giác đều
Đầu tiên, bạn cần biết độ dài của cạnh tam giác đều. Nếu không có thông tin này, hãy tìm cách tính hoặc đo đạc để lấy được giá trị cạnh.
Bước 2: Áp dụng công thức tính chiều cao
Sau khi có giá trị cạnh, hãy áp dụng công thức tính chiều cao cho tam giác đều:
$$h = a\frac{{\sqrt 3 }}{2}.$$
Ví dụ: Giả sử cạnh của tam giác đều là 6cm, chiều cao sẽ được tính như sau:
h = (6 * sqrt(3)) / 2
h = (6 * 1.73) / 2
h = 10.38 / 2
h = 5.19cm
Bước 3: Kiểm tra kết quả
Sau khi tính toán, bạn nên kiểm tra lại kết quả xem có hợp lý không. Chiều cao của một tam giác đều luôn nhỏ hơn cạnh của nó.
Cần thông tin nào để tính chiều cao của tam giác đều?
Để tính chiều cao của một tam giác đều, bạn chỉ cần biết một thông tin duy nhất: Độ dài của cạnh tam giác đều.
Nếu có thông tin về diện tích hoặc chu vi, bạn cũng có thể suy ra được độ dài cạnh và áp dụng công thức tính chiều cao.
Ngoài công thức tính chiều cao, dưới đây là một số công thức khác liên quan đến tam giác đều:
- Chu vi tam giác đều: C = 3a (với a là cạnh)
- Diện tích tam giác đều: S = (sqrt(3) * a^2) / 4 hoặc $$S = \frac{\sqrt{3} \cdot a^2}{4}$$
Những công thức này sẽ giúp ích cho việc tính toán và giải các bài toán liên quan đến tam giác đều.
Cách tính chu vi, diện tích, cạnh đáy, chiều cao hình tam giác
Tính chu vi tam giác
Công thức tính chu vi tam giác:
C = a + b + c
(với a, b, c là ba cạnh của tam giác).
Ví dụ: Cho tam giác ABC có cạnh a = 4cm, b = 5cm, c = 6cm. Chu vi của tam giác là: C = 4 + 5 + 6 = 15cm
Tính diện tích tam giác
Công thức tính diện tích tam giác:
S = (1/2) a h hoặc $$S = \frac{1}{2}ah.$$
(với a là cạnh đáy, h là chiều cao tương ứng).
Ví dụ: Cho tam giác ABC có cạnh đáy a = 6cm và chiều cao h = 4cm. Diện tích của tam giác là: S = (1/2) * 6 * 4 = 12cm^2
Tính cạnh đáy tam giác
Nếu biết diện tích và chiều cao, ta có thể tính cạnh đáy bằng công thức:
a = (2 * S) / h
Ví dụ: Cho tam giác có diện tích S = 18cm^2 và chiều cao h = 6cm. Cạnh đáy của tam giác là: a = (2 * 18) / 6 = 6cm
Kết luận
Tính đường cao của một tam giác đều là một bài toán đơn giản nhưng vô cùng quan trọng trong môn Toán học. Bằng cách áp dụng công thức h = (a sqrt(3)) / 2, chúng ta có thể dễ dàng tính được chiều cao của bất kỳ tam giác đều nào chỉ với thông tin về cạnh.
Ngoài ra, việc hiểu rõ các công thức tính chu vi, diện tích, cạnh đáy và chiều cao cũng giúp ích rất nhiều trong việc giải quyết các bài toán liên quan đến tam giác nói chung.
Hy vọng bài viết này đã cung cấp cho bạn những kiến thức bổ ích về cách tính chiều cao tam giác đều và nếu như có câu hỏi hoặc góp ý nào khác dành cho bài viết thì đừng quên để lại lời bình của bạn trong phần dưới đây.